Optikfunderingar - Försöker förstå

[Walle]

Jag har haft foto som hobby sen 2002. Trots det har jag aldrig satt mig in i hur objektiven fungerar rent optiskt. Eller jo, litegrann kan jag. Har väl fått hyffsat koll på det här med syn- och utlysningsvinklar, varför gluggar vinjetterar, och så. Men jag har ingen egentlig förståelse för hur optiska system fungerar. Jag hittade då en intressant artikel, väldigt basic men gav mig flera aha-upplevelser (hoppas jag..jag är ju inte säker på att jag har förstått allt helt rätt). Tror att jag har förstått skillnaden mellan en virtuell bild och en äkta/riktig bild (real image).

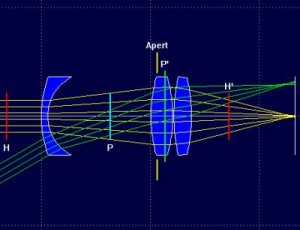
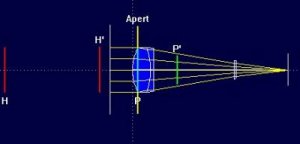
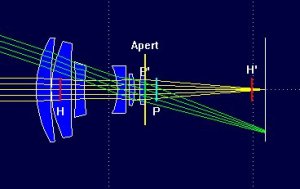
Jag hittade också en intressant java-applet, en virtuell optisk bänk där man kan sätta in olika linser och se påverkan på ljusstrålarna. Superbra för att förstå lite mer! Hittade även ett program som heter VOB (Virtual Optical Bench) i demoversion. Lite svåranvänt till en början, mycket kraftfullare än java-appletten. Appletten har t.ex. inte stöd för miniscus-linser (linser som är krökta åt samma håll på båda sidor, s.a.s.).

Jag har några funderingar dock:

1: Har jag förstått det rätt att en virtuell bild är när strålknippet divergerar eller är parallellt, och ögats konkava lins bryter detta strålknippe till en brännpunkt?

2: Vad är ett objektivs brännvidd? Är det brännvidden för hela systemet? Eller är det brännvidden för en del av systemet? Anledningen att jag undrar är att jag fick lära mig att brännvidden hos en lins är lika med avståndet mellan linsen och brännpunkten vid ett parallellt strålknippe. Jag får då inte ihop det med att man kan ha vidvinkelobjektiv med en brännvidd som är långt under registeravståndet. Jag förstår självklart att det sitter en eller flera linsgrupp/er som just ser till att fokus erhålls på fokalplanet, men jag får inte ihop hur ett objektiv med brännvidden 17mm t.ex. kan ha fokuspunkten 45.5mm bakom bajonetten. Därav min fundering om brännvidden som anges egentligen är brännvidden för en del av optiken, och att de/den bakre linsgruppen inte "räknas".
Edit: Eller är det så att ett objektiv har en bakre och en främre brännvidd, och att det är en främre som anges? Och att den bakre brännvidden är = avståndet mellan bakersta linselement och fokalplan för utdragsfokuserande objektiv, och att den varierar för innerfokuserande och frontfokuserande objektiv?

3: Jag har många gånger läst att strålknippen från oändligheten anses vara parallella, stämmer det? Då undrar jag hur det blir med ett vidvinkelobjektiv med stor bildvinkel? Jag menar, om vi tar ett fisheye med 180 graders bildvinkel som extremexempel, så kommer ju strålarna verkligen från helt olika håll. De yttersta strålarna har ju i princip vart på "kollisionskurs". Dessa kan väl inte anses vara parallella? När jag kollar på Canon Museum så kan man ju se blockschema för de olika objektivens konstruktion. Kollar man på vidvinklar så ser man att frontlinsen är konvex av miniscus-typ. Är det just för att strålknippet som träffar frontlinsen är konvergerande? Eller tänker jag fel här? Från en given punkt på motivet divergerar ju ljusstrålarna, men från frontlinsen sett måste ju strålknippet vara konvergerande? Jag känner att jag nog har rört ihop det här. Visst måste man hålla isär strålknippen från en punkt, och strålknippet som utgör själva bilden?

4: Apråpå fisheye så funderade jag på hur frontlinsen på ett fisheye-objektiv fungerar. För mindre extrema brännvidder så träffar ju ljus från varje given punkt på motivet hela frontlinsen (I princip såklart), men för en extremvidvinkel typ fisheye så kommer ju ljuset från de extrema vinklarna endast träffa "ena sidan" av frontlinsen, eftersom frontlinsen har så kraftig kurvatur. Är detta i princip samma som vinjettering skapad av att motljusskyddet "skuggar" frontlinsens kanter, så inte hela frontlinsen träffas av ljus från utsnittets ytterkanter? (Jodå, jag vet att det är en kraftig förenkling, att det egentligen är ingångspupillen det handlar om) Är det i.s.f. orsaken till att bilden blir rund? Att det altså är en väldigt kraftig form av vinjettering? Det känns inte helt rätt att det ska vara så, så jag tror det är fel. Men jag vet inte vad som är rätt

Det var väl de initiella funderingarna jag hade, men det lär komma fler

/Christoffer

 

[Frolicc]

Jag brukar älska att svara på fysikaliska frågor om tekniken som inte har något med att ta bilder att göra. Men nu gick du för långt, fattar inget! =)

Har inga svar, väntar på dem med spänning!

 

[Frolicc]

Tillägg.

En gång frågade en av mina kursdeltagare hur ett obejektiv fungerade. Började rita linser och bländare men efter ett tag började jag gå vilse i ljusstrålarna och gav upp förklaringsförsöket, mest för att jag inte kunde själv. =)

4:an verkar vara mest spännande.

 

[lusidor]

Hurra! Jag kan en sak! ;o)

Det gäller punkt 3)

Du har helt rätt i att du blandat samman två saker här. Ljus från olika delar av motivet är inte parallela. Men de bryts ju heller inte till samma punkt i bilden.

Strålar från samma punkt i "motivet", som träffar olika delar av linsen, bryts till samma punkt i bilden. Om denna punkt är oändligt långt bort så anses strålarna vara parallella.

 

[The_SuedeII]

Lite för trött just nu, men lite iaf...

Den "virtuella bilden är egentligen inte viktig - i ett verkligt sammanhang. Den är bara ett sätt att visualisera en brännpunkt när det inte finns någon. En divergerande lins som träffas av parallella ljusstrålar kommer ju SPRIDA ljusstrålarna - då finns det ingen "verklig" folkalpunkt på någon av linsens sidor. Den ena fokalpunkten är på ett oändlighetsavstånd och därmed "virtuellt". På andra sidan går ljus"strålarna" isär, och kommer alltså aldrig till en fokapunkt här heller. Men om man dra ut riktningen på spridningen i negativ riktning, dvs tillbaka mot utgångspunkten, oändlighetspunkten, så kan man här hitta en fokalpunkt på ett negativt avstånd. Efersom ett negativt avstånd är besvärligt i konstruktionssammanhang kan man visualisera fokalpunkten som "virtuell" istället. Den finns ju egentligen inte, den är en extrapolering av spridningen - baklänges.

Objektivets brännvidd är en kombinationsprodukt av många brännvidder, och egentligen är inte brännvidderna i sig självt speciellt viktiga... om man inte vill tillverka ett filmkamerazoom där det är viktigt att bildvinkeln och ändras när man fokuserar, och att fokuseringen inte ändras när man zoomar. Då bli rde inbördes relationerna helt plötsligt väldigt viktiga.

Ett normal fast objektiv kan nog oftast lättast förenklas till två brännvidder, en före och en efter bländaren. Kombinationen av dessa ger att en viss vinkel av området framför kameran/linsen projiceras på sensorytan, och genom att ta denna vinkel och jämföra med sensorn så kommer man fram till den "brännvidd" som man skriver på objektivet. en 36mm bred sensor som får med 39º på bredden av rymden framför ingångspupillen när fokus ligger på oändlighet är ett "50mm-objektiv".

Saken kompliceras ytterligare av att brännvidderna är "virtuella" på så sätt att de påverkas av var bländaren fysiskt placeras. Om du har ett objektivlock du kan offra, och ett normalobjektiv på 50-85mm med stor bländare (1.8 eller helst större) så kan du göra ett 10-15mm stort hål exakt mitt i objektivlocket, köra objektivets inbyggda bländare vidöppet och jämföra hur brännvidden förändras... Hålet i objektivlocket har nu blivit bländare, och du har byggt om objektivets egenskaper fullständigt eftersom du har flyttat bländarens position. Även om du inte så mycket som petat på de fysiska glasen i objektivet...

Vidvinklar är ofta retrofokala, dvs de har lång brännvidd på baksidan om bländaren och kort brännvidd på framsidan (JA, Lennart, jag vet att detta inte är den tekniskt korrekta definitionen...!) -Just för att objektivet ska "få plats". Detta ger (iaf gav) ofta problem med CA, eftersom CA i stort sett alltid är lättast att korrigera i ett symmetriskt objektiv - objektiv som är ganska lika på fram- och baksida, bara spegelvända. Canon-objektiven du nämnde har antagligen den konstruktion de har pga detta, och en modern motsvarighet finns idag för 4/3-systemet - Oly50-makron har en konkav främmersta linsyta... Jag tror bakersta linsytan är konkav också - men detta är ett mycket avancerat 11/10-objektiv som antagligen är retrofokalt för maximal prestanda på 4/3-systemet - som är mycket vinkelkänsligt.
Retrofokala objektiv används ganska långt upp i brännvidderna på moderna objektiv eftersom sensorer INTE tycker om ljus som kommer in mot sensorytan med för stor vinkel - helst ska allt ljus komma rakt framifrån...

"Parallella" strålknippen som du nämnde är ju inte ALLT ljus som ska projiceras på sensor samtidigt. Oändlighetetsfokus, eller fokus på kollimerat ljus innebär att ALLA punkter på horisonten avger ljus som kommer fram i "parallella" knippen till frontlinsen. Det innebär inte att alla punkter är på samma plats, utan att ljuset från var och en av den anländer till objektivet i parallell formation, varje knippe för sig.

Sen finns det ju egentligen inget sådant som "fotoner" eller "strålgångar", men det är en helt annan sak... För praktiskt optik kan detta kvitta fullständigt fram till att man börjar diskutera diffraktion och "gratings". Modellen fungerar alldeles "strålande" höhöh. Börjar bli trött nu.

Bluaäh.... Vinjettering. Fisheye. Hmmm. Ett ganska stort ämne, men vi kan ta grunderna iaf.

Vinjetteringen består förenklat i fyra grund-delar. cos4-regel för främre pupill, cos4-regel för den bakre pupillen, vinkeleffektivitet i refraktion/reflektion samt mekanisk vinjettering. Sen ska vi blanda in sensorn också, kanske som en femte del - och den är till stor del också medskyldig till vinjetteringen.

Cos4-regeln är hur ytan på pupillen förändras av vinkel. Den främre pupillen släpper "in" ljus i systemet, den bakre pupillen släpper "ifrån" sig ljuset som förhoppningsvis ska fokuseras på sensorn. Pupillerna är runda, eller åtminstone ganska runda (bländarbladen påverkar ju).

Ta en vanlig assiett och håll upp den framför dig på armlängds avstånd med "ätytan" riktad exakt vinkelrätt mot dig. När du håller den så här upptar den en viss rymdvinkel av ditt seende, den har en viss "ljuspåverkan" som beror på dess yta som kombinerat med din armlängd blir en viss rymdvinkel. Om du nu VRIDER tallriken 15º i sidled så att du tittar på den lite snett från sidan så har ytan, och därmed rymdvinkeln MINSKAT. I objektivet betyder detta att ytan som släpper igenom ljus minskar med vinkeln du titta på pupillen från. 0º ger störst genomsläpp, 30º ger ett betydligt mindre genomsläpp. Ytan minskar förenklad med (cos(vinkel))^4, därmed namnet på regeln - "cos4".

Mekanisk vinjettering - om nu pupillerna i ALLA vinklar som det är meningen att det ska gå att göra kan ses utan att de skyms av något finns det ingen mekanisk vinjettering. Alla punkter på sensor ska kunna "se" hela utgångspupillen, alla punkter som täcks av bildvinkeln framför objektivet ska kunna se hela ingångspupillen.

Refraktion/reflektion:
Ju mer vinkelrätt mot en glasyta en ljusstråle träffar, desto mer "går igenom" ytan utan att reflekteras, Lägger man vinkeln ner studsar mer, mindre går igenom. Sammantaget på alla lins/luftytor som en strålgång passerar igenom i ett normalt objektiv kan detta göra en del skillnad mellan "rakt på" och "lite från sidan" - man ska addera alla vinklar för att få fram en summa för förlusterna. Summan är mycket lägre för mittdelarna av bilden än för ytterhörnen av bilden.

Sensorn - orkar jag inte just nu. Macka och sova.

Lennart kan säkert korrigera en hel del av det jag skrivit om han nu vill det, men vissa små lögner "på vägen" kan hjälpa förståelsen. Vill du ha en komplett beskrivning kan jag rekommendera lite böcker - men de är både svindyra och ganska träiga. Natti.

 

[Pupillen]

Saken kompliceras ytterligare av att brännvidderna är "virtuella" på så sätt att de påverkas av var bländaren fysiskt placeras. Om du har ett objektivlock du kan offra, och ett normalobjektiv på 50-85mm med stor bländare (1.8 eller helst större) så kan du göra ett 10-15mm stort hål exakt mitt i objektivlocket, köra objektivets inbyggda bländare vidöppet och jämföra hur brännvidden förändras... Hålet i objektivlocket har nu blivit bländare, och du har byggt om objektivets egenskaper fullständigt eftersom du har flyttat bländarens position. Även om du inte så mycket som petat på de fysiska glasen i objektivet...

Ett bra och lärorikt experiment (fast brännvidden ändras inte;-) inga nya vägar öppnas ju för ljusstrålarna utan tvärtom begränsar vi ju flödet, det är därför ”bara” ett annat urval av de tillgängliga vägarna genom objektivet som gör den stora skillnaden) Det kan vara värt att notera att om vi vill kunna använda ett mycket litet objektivlockshål utan fysisk vinjettering måste vinklarna från hålet ut till den ordinarie ingångspupillens periferi vara minst lika stor som objektivets ordinarie synvinkel. Det är alltså ingångspupillens storlek och placering i objektivet som bestämmer hur stor synvinkel och hur liten vinjettering vi kan få med en sådan här objektivlockshålkamera.

Nu kommer vi snubblande nära problemkärnan i fråga 4 fast från ett annat håll, i vidvinkelfallet är det ju istället frontlinsen som kan sägas motsvara objektivlockshålet och är den stora öppningen medan ingångspupillen inne i objektivet är det lilla hålet. I båda fallen är det dock TVÅ hål med ett avstånd emellan och det är detta avstånd och hålens inbördes storleksförhållanden som begränsar den möjliga synvinkeln. Specialfallet med två lika stora hål (när frontlinsen och ingångspupillen är lika stora) på långt avstånd från varandra fungerar bara med små synvinklar och stora hål, d.v.s. förhållandevis ljusstarka teleobjektiv, redan ljusstarka normaler har så pass stora synvinklar att avståndet mellan hålen måste vara rätt litet.

Fråga 2:

Objektiv har i o f s två brännvidder fast de är i fotografiska sammanhang normalt lika stora och har alltså inte med detta att göra.

Brännvidderna ifråga mäts egentligen från objektivet främre och bakre huvudpunkter (brukar benämnas H respektive H´) till respektive brännpunkter (F respektive F´). Dessa huvudpunkter behöver inte befinna sig inne i objektivet utan man kan mycket väl konstruera detta så att den bakre huvudpunkten hamnar bakom den bakersta linsen så att spegeln får plats om brännvidden är kort. Även en vanlig enkel lins behöver inte vara speciellt extremt meniskformad för att huvudpunkterna ska hamna utanför själva linsen, redan med en plankonvex lins hamnar den ena huvudpunkten exakt på den plana ytan.

Tillägg:

Ett annat sätt att försöka svara på fråga 4 är att hänvisa till glasögon, låt ditt eget ögas pupill motsvara vidvinkelobjektivets ingångspupill (som ju finns ett gott stycke in i objektivet på samma sätt som vi p g a ögonfransarna har glasögonglaset långt framför vår pupill) så inser vi att glasögonglasets storlek påverkar hur stort synfält vi kan få, d.v.s. vårt ögas vidvinklighet. Exemplet kan verka lite missvisande eftersom ögats pupill ju flyttas när vi sneglar åt sidorna men något liknande sker faktiskt med våra vidvinklars ingångspupiller (titta in i ett extremt vidvinkelobjektiv framifrån och ”möt dess blick”, när vi flyttar oss bort från optiska axeln (eller vrider objektivet) ser man rätt lätt att ingångspupillen ser ut att följa med, vridas, förstoras och deformeras.

 

[The_SuedeII]

Jag tänkte nog att du skulle lägga till lite... -Nej bildvinkeln färändras inget, men däremot förändras ALLA parametrar för objektivet i övrigt (CA, LoCA, komatisering, SA osv..), eftersom det är nya, begränsade strålgångar som används. Det är en nerbländning på ett nytt ställe i optiken.

Lennart - kan alltså den konkava främmersta ytan i Olympus-makrona bero på att man vill flytta fram den främre huvudpunkten så att man får ett bättre arbetsavstånd?

 

[Walle]

Tack för era svar! Jag har läst igenom en gång, men jag är på tok för trött ikväll dessvärre (sömnbrist), så jag får återkomma imorgon!

Jag ska prova att "flytta fram" bländaren på mitt 85/1.2, det lär väl synas oerhörd markant skillnad med den kan jag tänka mig? Kan man på något sätt lista ut vilket f/stop man får, så man kan ta en bild med motsvarande inställning på den interna bländaren? För inte kan man väl räkna som vanligt? Altså Bländare = Brännvidd / Ingångspupill? Med ett riktigt snabbt test verkar det som att man kan det, gjorde ingen exakt beräkning, men ett hål på 12 mm gav liknande exponering som f/7.1. Men det var med en ljus kartongskiva handhållen framför handhållen 5D + 85/1.2 i mörkt vardagsrum. Jag trodde inte att man skulle kunna räkna med den formeln när bländaren ligger utanför det optiska systemet (eller det kanske den inte gör om den ligger precis framför frontlinsen?), men jag tycker mig ha verifierat att man kan det.

Men nu känns ögonen som grus, jag får försöka att inte fundera så mycket på det här nu tills i morgon, så jag kan sova

 

[Pupillen]

Jodå, det går bra att använda den vanliga formeln. Den enda skillnaden med att ha bländaren framför objektivet är att ingångspupillen då inte längre är en virtuell bild av bländaren utan är lika med den rent fysiska bländaren och lätt kan mätas med skjutmått

Jag tycker förresten absolut att hålet ingår i det optiska systemet även om det råkar vara lite ovanligt placerat.

 

[Pupillen]

Lennart - kan alltså den konkava främmersta ytan i Olympus-makrona bero på att man vill flytta fram den främre huvudpunkten så att man får ett bättre arbetsavstånd?

Vet inte, men tror att det är att dra lite för långtgående slutsatser, det finns i alla fall ingen så uppenbar fördel att jag kan upptäcka den i alla fall

Flera av Leicas vidvinklar har ju också konkava frontlinser och de har ju inte mycket gemensamt med Olympus 50:a (varken makro eller "rak strålgång").

 

[lusidor]

Flera av Leicas vidvinklar har ju också konkava frontlinser och de har ju inte mycket gemensamt med Olympus 50:a (varken makro eller "rak strålgång").

Ville minnas att en gammal Canon 35:a jag ägde en gång hade konkav frontlins - och minsann fanns den inte att beskåda på muséet!

Står bl a så här om optiken "(...) A inverted telephoto lens type wide angle lens like this lens, having negative power like a concave lens for front lens group and positive power like a convex lens for rear lens group (...)". Vet inte om det hjälper oss förstå fördelen med konkava frontlinser, men det var ju ett snyggt diagram! ;o)

 

[Walle]

Nu har jag läst igenom era svar igen några gånger, samt att jag har suttit halva helgen och experimenterat i VOB, och nu börjar bitarna trilla på plats!

Jag insåg ju rätt snabbt att jag blandade ihop "strålvinklarna" från en punktkälla på oändligheten med optikens synvinkel. Jag har upprepat den tankevurpan ett antal gånger, men att simulera en enkel optik i VOB, och animera "ljusstrålarna" så de sveper fram och tillbaka över synvinkeln hjälpte min hjärna mycket



ca 28mm brännvidd, avstånd mellan sista linsytan och filmplan ca 55mm. Det gröna ljusknippet kommer från ca 32 grader. "Sensorn" är 36mm. Det känns som att jag börjar förstå det här med retrofokala vidvinklar. Man ser för övrigt tydligt problemet med comatisk aberration här (Det gröna strålknippet fokuserar inte på samma avstånd. Edit: Det är bara grönt för illustrationens skull, det ska inte föreställa grönt ljus). Inzoomat en liten aning är även sfärisk aberration väldigt tydlig.

Nu är ju inte optiken ovan något vidunder direkt, f/6.0 ungefär sa programmet innan det kraschade. Men kan man se strålgången som hyffsat representativ? Då tänker jag främst på hur man ser att bara en del av frontlinsen nyttjas för varje "strålknippe" från en punktkälla. Det känns som att det går hand i hand med förklaringarna jag har fått på ingångspupillen kontra frontlinsens storlek / glasögonen. I övrigt vet jag såklart att optik är betydligt mer avancerade än så här, men jag tänker som sagt främst på brytningen genom frontlinsen. Jag tycker även det stämmer med vad jag ser om jag ställer mig och tittar in genom frontlinsen på en vidvinkel. Då ser ju ingångspupillen ut att vara en bit in och ganska liten (såklart beroende på objektiv), och altså ser jag mycket glas där en tänkt ljusstråle från mitt öga inte skulle brytas så den passerade genom ingångspupillen.

Finns det normalt alltid ett "naturligt" ställe att placera bländaren när man konstruerar ett objektiv? När jag experimenterar i VOB så märker jag hur "aperture" flyttar på sig när jag ändrar olika parametrar. Den visar väl helt enkelt vart det "smalaste" (ur en strålgångssynvinkel) stället genom optiken? Är det där, eller så nära som möjligt, man skulle placera en fysisk bländare, eller styrs det av helt andra parametrar?

Siffror och formler kommer jag nog inte sätta mig och traggla, men jag är är en sådan som väldigt gärna vill förstå principerna (det gäller inte bara optik, utan det mesta. Jag är fruktansvärt vetgirig av mig).

Men jag funderar på att bygga ett enkelt objektiv (Jag tänker fixfokus och fast bländare), bara för att få ännu bättre incitament till att förstå ännu bättre. Ett objektiv kring 100mm brännvidd byggd i EK vore väl något? Självklart skulle det knappast bli särskilt skarpt och jag skulle få allehanda optiska problem på köpet..men det skulle säkerligen vara lärorikt!

 

[Walle]

Kan det förresten vara som så att det är en fördel att frontlinsen är kraftigt miniskformad ur vinjetteringssynpunkt? För att "anslagsvinkeln" för strålknippen från bildens periferi då skiljer sig mindre från "anslagsvinkeln" för strålknippen från bildens mitt? Tänker då på Refraktion/reflektion.

 

[lusidor]

Jag har alltid tänkt mig att bländaren måste sitta där strålarna från ytterkanterna på bildcirkeln korsar varandra. I ditt exempel ovan ser det lite märkligt ut, när bländaren ska sitta inne i en lins ;o). Men det beror förstås på att det är ett förenklat exempel med få linser.

För övrigt tycker jag det är kul att du gräver i det här, Walle! Jag gillar också att förstå principerna för allt, trevligt att hänga på i dina funderingar!

 

[Walle]

Leif, det är mycket möjligt att jag totalt har missförstått hur man designar ett objektiv Det skulle liksom inte förvåna mig. I bilden ovan är det dock programmet själv som markerar med linjen för "Aperture" vart den begränsande diametern finns (om jag har förstått allt rätt, det vill säga). Det är helt enkelt där det rent optiskt är som "trängst", men rent fysiskt skulle man nog placera bländaren någon annan stans Vi får se om Lennart eller Joakim bringar klarhet i den frågan

Just det där med korsande "strålar" är också något som jag har funderat på. När jag har suttit och experimenterat med olika enkla optikkonstruktioner så har "strålarna" (jodå, jag är medveten om att ljus är elektromagnetism i vågform och inte strålar, men som sagt, för pedagogiskt bruk verkar strålar funka utmärkt aldrig korsat varandra innuti optiken. När jag har kollat på olika vedertagna optikkonstruktioner så verkar det som att i vissa konstruktioner så korsar strålarna aldrig varandra, men i vissa andra så gör dom det. Låt mig illustrera med ett exempel:



En enkel telekonstruktion, om jag har förstått det hela rätt. Brännvidden är 210mm. Fokus ligger 57mm bakom bakersta linsytan. Både H och H' ligger framför frontlinsen. Bländaren är f/2 med 50mm ingångspupill (Samma som frontlinsdiametern, vad drar jag för slutsats av detta?). Jag lekte för övrigt loss med en "achromatic double" som frontlins. Den konvexa linsytan har lägre brytningsindex och högre Abbe-tal än den konkava.

Jag kan glädjande meddela att jag äntligen har förstått varför skärpedjupet blir mindre med större bländare Det är något som jag har funderat lite smått på i flera år, men här om dagen kom det till mig och då blev jag nästan irriterad över att jag inte har kommit på det tidigare De tänkta "trattarna" blir ju smalare med en mindre bländaröppning, då blir ju CoC mindre. Har man då en mindre bländare blir ju alla "trattar" smalare, oavsett avstånd.

 

[Walle]

Jag tycker mig för övrigt ha gjort iaktagelsen att det inte alls är "främre nodpunkt" man ska rotera optiken rund vid panoramafotografering, utan ingångspupillens virtuella läge. Stämmer det?

Men vafasiken..ny sida blev det med det här inlägget. MIssa nu inte de sista inläggen på förra sidan, som man så ofta gör när det har blivit en ny sida i en tråd. Det vore trist om de inläggen glömdes bort, eftersom jag hade en del funderingar där

 

[lusidor]

Det jag menar är strålknippen från olika delar av motivet - återigen ;o). Eftersom bilden spegelvänds så kommer det alltid att finnas ett ställe i optiken där strålar från olika delar av motivet korsar varandra.

Jag vet inte att det förhåller sig så, men jag har alltid föreställt mig att det är i detta plan som bländaren placeras. Det ska bli intressant att höra "domen" ;o).

 

[Walle]

Ah, du menade så ja

Nu när du säger det så låter det självklart Annars hamnar vi väl i det scenariot som Joakim visade med "objektivlocket"?

 

[The_SuedeII]

Hinner inte skriva så mycket nu - kanske senare ikväll - men det som programmet sätter ut som "aperture position" är det plan i optiken som bestämmer "clear aperture" i en obegränsad optik. En "obegränsad optik" består BARA av linserna och dess infattningar, den har helt enkelt ingen bländare.

Ofta vill man flytta denna punkt för att man vill styra huvudplanen i optiken, ungefär som mitt exempel med en "ny" bländare placerad i objektivlocket innan. Man förändrar väldigt mycket av de grundläggande aberrationerna genom att flytta bländarpositionen.

Det som du angav som "CA" innan i det föra exemplet är egentligen "field curvature" - att optiken inte fokuserar hela fältet på samma avstånd. Optimalt för fotobruk är antingen ett helt plant fokusfält (en tegelvägg fotograferad från en exakt 90º vinkel ska vara väl fokuserad över hela bildplanet) eller att fokusplanet bockar lite in mot dig så att "bästa fokus" ligger lite närmre dig i kanterna av bilden än i mitten av bilden. Ditt exempel verkar ha ganska extrem fältförvrängning, om mitten av bilden är fokuserad på oändlighet skulle du nog ha skärpa på 4-5m avstånd längst ut i kanterna av bilden.

 

[Walle]

Aha, jag blandade ihop field curvature och comatic abberation (jag menade inte cromatic abberation). Fast visar inte exemplet både och? Är inte "comatic abberation" hur ljusstrålar som ska brytas till samma punkt sprids ut (och bildar "kometformen")?

Hursomhelst så tror jag att det gick upp ett litet ljus nyss



När man tittar på den bilden så tycker jag det blir oerhört uppenbart hur optikens egenskap påverkas markant av bländarens placering. Om vi tänker oss att vi placerar bländaren mellan element 2 och 3 (från vänster altså, om inte det är självklart) så skulle vi väl oerhört snabbt få en vinjettering och därefter en förminskad bildcirkel vid nedbländning? Men om vi placerar bländaren där "Apert" ligger så får vi mer eller mindre bara ett ökat skärpedjup? (Jag förstår självklart att optiken inte är optimal. Och bortse från att brännvidden tycks vara 5mm om man kollar på H', det är bara optimeringen som har buggat ur. Nånstans runt 42mm är brännvidden i exemplet)

Tänker jag rätt?